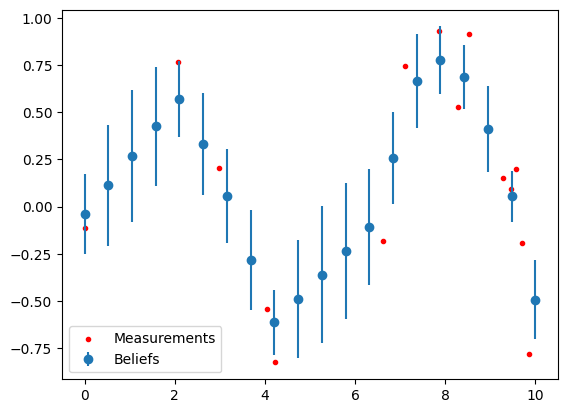
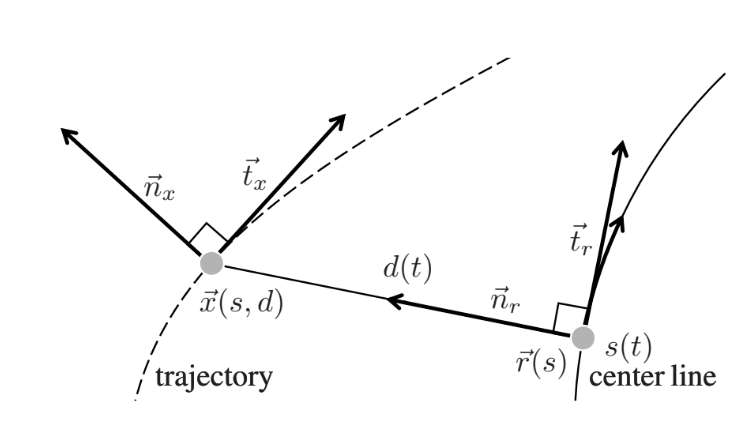
Line Fitting Using Gaussian Loopy Belief Propagation

Gaussian Belief Propagation is a variant of Belief Propagation and used for inference on graphical models if the underlying distribution is described as a Gaussian.

This article describes the implementation of the inference of a piecewiese separated Line using Gaussian Loopy Belief Propagation. The example is taken from A visual introduction to Gaussian Belief Propagation. I work here with a stripped version of Joseph Ortiz’s notebook in hope to make the implementation more comprehensible. My contribution is to explain what is going on in the code and relate it to the formulas and algorithms given in the introduction as the notebook contains mostly only code (as of now).

Simple Noise Reduction with Loopy Belief Propagation

I want to continue my previous post with a (useful) example to get more a feel how to use Loopy Belief Propagation in practice.

The aim is to remove noise from an image - which is only a toy example.

Loopy Belief Propagation - Python Implementation

This is about how to implement Loopy Belief Propagation in Python and to understand the calculations in detail.

Path Planning with Quintic Functions in Frenét Coordinate System

This is an introduction on how to compute a driving path for an autonomous vehicle. In this article, I focus only the trajectory creation. Obstacle perception and avoidance shall be out of scope.

The idea comes from paper 

Werling, M., Ziegler, J., Kammel, S., & Thrun, S. Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenét Frame. 

I would like to show in detail how this is put into practice. I will omit all further references to this paper in this article, as the ideas coming from there.

Maneuvers of a car shall be as smooth as possible. Hard turns or hard deceleration are only required in dangerous situations. Thus, we need a function that minimizes Jerk, which is used in physics to describe how much the acceleration changes.